Lý thuyết phương trình đường tròn qua phép tịnh tiến
Theo lý thuyết, để viết phương trình đường tròn qua phép tịnh tiến ta có 2 cách sau:
- Sử dụng biểu thức tọa độ tìm phương trình đường tròn
- Sử dụng tính chất để viết phương trình đường tròn
Ví dụ phương trình đường tròn qua phép tịnh tiến
Để hiểu rõ hơn cách làm ta tham khảo ví dụ tìm phương trình đường tròn đi qua phép tịnh tiến sau:
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình: \(x^2+y^2-2x+4y-4=0\). Tìm ảnh của đường tròn (C) qua phép tịnh tiến theo \(\vec{v}=(-2,3)\)
phuong-trinh-duong-tron-qua-phep-tinh-tien-theo-vec-to-v
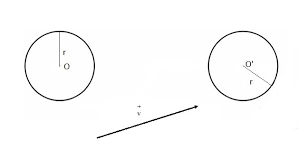
Cách 1: Sử dụng biểu thức tọa độ tìm phương trình đường tròn
Giả sử M(x;y) là điểm bất kì thuộc đường tròn (C) và M'(x’;y’) thuộc đường tròn (C’) là ảnh của điểm M qua phép tịnh tiến theo vectơ \(\vec{v}=(-2,3)\)
Theo biểu thức tọa độ của phép tịnh tiến ta có:
\(x’- x = ay’- y = b \Leftrightarrow x = x’ – ay = y’ – b\)
Thay a = – 2, b = 3 ta được \(x = x’ + 2y = y’ – 3\)
Thay x; y ở trên vào phương trình của đường tròn (C) ta được:
\((x’+2)^{2}+(y’−3)^{2} − 2(x’+2) + 4(y’−3) − 4 = 0\)
\(\Leftrightarrow x’^{2}+y’^{2} + 2x’ – 2y’ – 7 = 0\)\(\Leftrightarrow(x′+1)^2+(y′−1)^2=9\)
Vậy đường tròn (C’) có phương trình là: \((x′+1)^2+(y′−1)^2=9\)
Cách 2: Sử dụng tính chất để tìm phương trình đường tròn
Chúng ta đã biết tính chất: Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.
Do đó ảnh của đường tròn (C) sẽ là đường tròn (C’) có cùng bán kính với đường tròn (C). Việc chúng ta cần tiến hành tiếp theo là tìm tâm của đường tròn (C’). Tâm của (C’) lại là ảnh của tâm đường tròn (C) qua \(v⃗\)
Đường tròn (C) có tâm là I(1;-2) và bán kính r=3
Gọi (C’) là ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ \(v⃗\) và I'(x’;y’) là ảnh của tâm I qua phép tịnh tiến theo vectơ \(v⃗\) .
Ta có r’ = r = 3
Ta có: \(x’-x=a y’-y=b \Leftrightarrow x’=x+a y’=y+b\)
Thay x = 1, y = -2 ta được
\(x’ = 1 – 2y’= -2 + 3 \Leftrightarrow x’ = -1y’ =1\)
Vậy tọa độ của I’ là: I'(-1;1)
Đường tròn (C’) có tâm là I'(-1;1) và bán kính r = 3 có phương trình là:
\((x′+1)^2+(y′−1)^2=9\)
Trên đây là bài viết tổng hợp kiến thức về phương trình đường tròn qua phép tịnh tiến. Nếu có băn khoăn, thắc mắc hay đóng góp cho bài viết các bạn để lại bình luận bên dưới nha. Cảm ơn các bạn! Đừng quên chia sẻ nếu thấy hay nhé <3