Định nghĩa trung điểm là gì? Cách chứng minh trung điểm?

Chứng minh trung điểm là một dạng toán cơ bản nhưng quan trọng trong chương trình toán Trung học Cơ sở. Vậy cụ thể trung điểm là gì? Cách chứng minh trung điểm lớp 8 lớp 9 có gì giống và khác nhau? Cách giải bài toán chứng minh o là trung điểm ef?… Trong bài viết dưới đây, DINHNGHIA.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề trên, cùng tìm hiểu nhé!

Trung điểm là gì?

Trung điểm \( M \) của đoạn thẳng \( AB \) là điểm nằm giữa \( A,B \) và cách đều \( A,B \) hay \( MA =MB \). Trung điểm của đoạn thẳng \( AB \) còn được gọi là điểm chính giữa của đoạn thẳng \( AB \)

***Chú ý: Điểm \( M \) nằm giữa hai điểm \( A,B \) \(\Leftrightarrow MA+MB=AB\)

Những cách chứng minh trung điểm phổ biến và điển hình

Để chứng minh một điểm là trung điểm của một đoạn thẳng thì chúng ta cần sử dụng các tính chất hình học có liên quan đến trung điểm. Dưới đây là một số cách CM trung điểm cơ bản.

Cách chứng minh trung điểm lớp 6 – chứng minh theo định nghĩa

Để chứng minh điểm \( M \) là trung điểm của đoạn thẳng \( AB \) thì ta cần chứng minh đồng thời \( M \) nằm giữa \( A,B \) và \( MA+MB \)

Ví dụ:

Cho đoạn thẳng \( AB =8cm \) có \( M \) là trung điểm \( AB \). Trên \( AB \) lấy hai điểm \( C,D \) sao cho \( AC=BD=3cm \). Chứng minh \( M \) là trung điểm \( CD \)

Cách giải:

Vì \( M \) là trung điểm \( AB \) nên \( MA =MB =4cm \)

Vì \( M,C \) cùng phía với \( A \) mà \( AM > AC \) nên \( C \) nằm giữa \( AM \)

\(\Rightarrow MC =MA-CA = 1cm\)

Tương tự ta có \( MD =1cm \)

Mặt khác : \(CD= AB-AC-BD =2cm\)

Như vậy ta có :

\(\left\{\begin{matrix} MC =MD =1cm\\ MC + MD =CD \end{matrix}\right.\)

\(\Rightarrow M\) là trung điểm \( CD \)

Cách chứng minh trung điểm lớp 7 – dựa vào các tính chất của tam giác

Để chứng minh theo cách này thì trước hết chúng ta cần nắm vững các tính chất liên quan đến trung điểm trong tam giác.

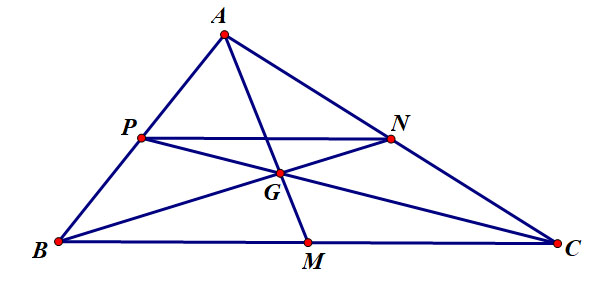
Cho tam giác \( ABC \) với \( M,N,P \) lần lượt là trung điểm của \( BC, CA, AB \)

Khi đó:

\( AM,BN,CP \) lần lượt được gọi là các đường trung tuyến của cạnh \( BC,CA,AB \) . 3 đường trung tuyến đồng quy tại điểm \( G \) được gọi là trọng tâm của tam giác \( ABC \) . 3 đoạn thẳng \( MN,NP,PM \) được gọi là các đường trung bình của tam giác \( ABC \)

• Tính chất trọng tâm: Nếu \( G \) là trọng tâm tam giác \( ABC \) thì \( AG,BG,CG \) lần lượt đi qua trung điểm của \( BC,CA,AB \) . Đồng thời : \(\frac{AG}{AM}=\frac{BG}{BN}=\frac{CG}{CP}=\frac{2}{3}\)

• Tính chất đường trung bình: Nếu \( MN \) là đường trung bình của tam giác \( ABC \) thì \( MN \) song song và bằng \(\frac{1}{2}\) cạnh đáy tương ứng.

Ví dụ:

Cho tam giác \( ABC \) có  \( AB >BC \) . \( BE \) là phân giác và \( BD \) là trung tuyến. Đường thẳng qua \( C \) vuông góc với \( BE \) cắt \( BE, BD, BA \) lần lượt tại \( F, G , K \)  \( DF \) cắt \( BC \) tại \( M \). Chứng minh rằng: \( M \) là trung điểm đoạn \( BC \)

Cách giải:

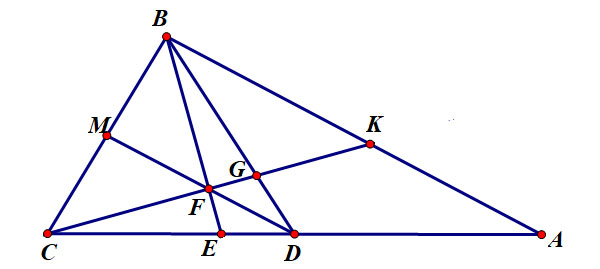
Xét \(\Delta BCK\) có

\(BF\) vừa là đường cao, vừa là phân giác nên \(\Delta BCK\) cân tại \( B \)

\(\Rightarrow BC=BK\) và \( BF\) là trung tuyến

\(\Rightarrow CF=FK\).

Xét \(\Delta CKA\) có

\(CF=FK ;CD=DA\) \(\Rightarrow FD\) là đường trung bình

\(\Rightarrow FD//AB\Leftrightarrow MD//AB\)

Mà \(CD=DA\) nên \(\Rightarrow \frac{CM}{CB}=\frac{CD}{CA}=\frac{1}{2}\)

\( \Rightarrow M \) là trung điểm \( BC \).

Cách chứng minh trung điểm lớp 8 – dựa vào tính chất tứ giác đặc biệt

Trong phần này chúng ta sẽ sử dụng một số tính chất trung điểm của các tứ giác đặc biệt như sau

• Đường trung bình hình thang

Cho hình thang \( ABCD \) hai đáy là \( AB,CD \). Khi đó \( MN \) được gọi là đường trung bình của hình thang \( ABCD \) \(\Leftrightarrow \left\{\begin{matrix} MN \parallel AB \\ MN =\frac{AB+CD}{2} \end{matrix}\right.\) và \( M,N \) là trung điểm của \( AB, BC \)

• Đường chéo hình bình hành

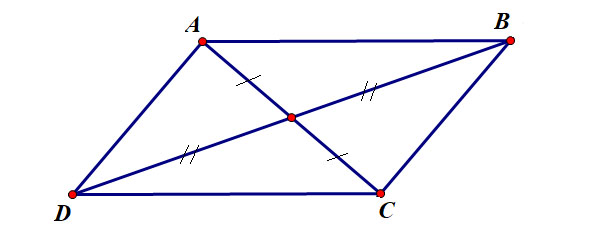
Cho hình bình hành \( ABCD \) với hai đường chéo \( AC,BD \) . Khi đó \( AC \) cắt \( BD \) tại trung điểm của mỗi đoạn.

***Chú ý: Hình vuông, hình chữ nhật , hình thoi là các trường hợp đặc biệt của hình bình hành nên cũng có tính chất nêu trên

Ví dụ:

Cho hình bình hành \( ABCD \) với \( I \) là giao điểm của \( AC,BD \). Lấy \( M \) là điểm bất kì nằm trên \( CD \) . \( MI \) cắt \( AB \) tại \( N \). Chứng minh rằng \( I \) là trung điểm [/latex] MN [/latex]

Cách giải:

Vì \( ABCD \) là hình bình hành mà \( I \) là giao điểm của hai đường chéo nên ta có : \( DI = MI \)

Xét \(\Delta DIM\) và \(\Delta BIN\) có :

\(\widehat{DIM}= \widehat{BIN}\) ( hai góc đối đỉnh )

\( DI = BI \) ( chứng minh trên )

\(\widehat{MDI}= \widehat{NBI}\) ( hai góc so le trong )

Vậy \(\Rightarrow \Delta DIM = \Delta BIN\) ( góc – cạnh – góc )

Vậy \(\Rightarrow IN=IM\) hay \( I \) là trung điểm \( MN \)

Cách chứng minh trung điểm lớp 9 – dựa vào các tính chất của đường tròn

Trong phần này chúng ta sẽ sử dụng quan hệ giữa đường kính và dây cung trong đường tròn:

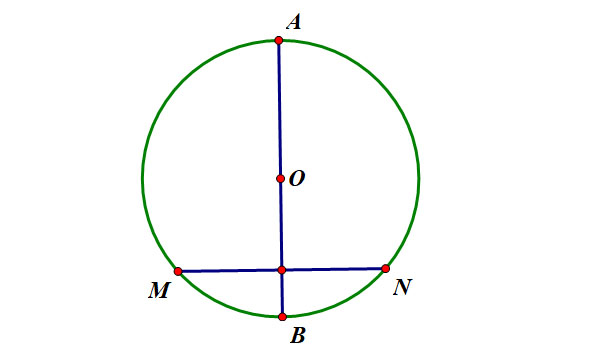
Cho đường tròn tâm \( O \) đường kính \( AB \). \( MN \) là một dây cung bất kì của đường tròn. Khi đó, nếu \(AB \bot MN \Rightarrow\) \( AB \) đi qua trung điểm của \( MN \) và ngược lại , nếu \( AB \) đi qua trung điểm của \( MN \) thì \(AB \bot MN\)

Ví dụ:

Cho tam giác \( ABC \) nhọn \( (AB < AC) \) nội tiếp đường tròn \( (O) \) . Tiếp tuyến tại \( A \) và \( B \) của \( (O) \) cắt nhau tại \( M \). Kẻ cát tuyến \( MPQ \) của \( (O) \) ( \( P \) nằm giữa \( M \) và \( Q \)) song song với \( BC \) cắt \( AC \) tại \( E \) . Chứng minh rằng \( E \) là trung điểm \( PQ \)

Cách giải:

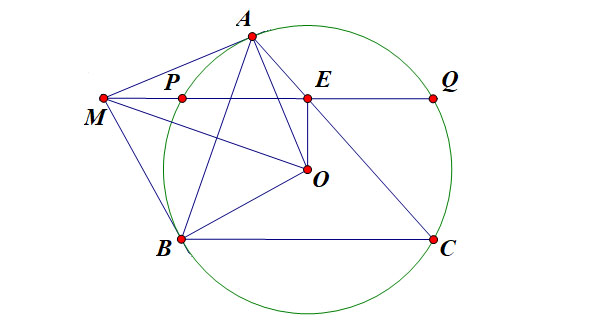
Vì \( MA , MB \) là các tiếp tuyến kẻ từ \( M \) của đường tròn \( (O) \) nên \(\Rightarrow MA =MB\)

Xét \(\Delta MAO\) và \(\Delta MBO\) có

\( MA =MB \) ( chứng minh trên )

\( MO \) chung

\( OA =OB \) ( bán kính \( (O) \) )

Vậy \(\Rightarrow \Delta MAO = \Delta MBO\) ( cạnh – cạnh – cạnh )

\(\Rightarrow \widehat{MOA}=\widehat{MOB}\)

\(\Rightarrow \widehat{MOA}=\frac{\widehat{AOB}}{2} \hspace {1cm} (1)\)

Vì \(PQ \parallel BC \Rightarrow \widehat{MEA}=\widehat{BCA}\) ( đồng vị )

Mà \(\widehat{BCA}=\frac{\widehat{AOB}}{2}\Rightarrow \widehat{MEA}=\frac{\widehat{AOB}}{2} \hspace{1cm} (2)\)

Từ \((1)(2)\Rightarrow \widehat{MEA}=\widehat{MOA}\)

\(\Rightarrow\) tứ giác \( MOEA \) nội tiếp

\(\Rightarrow \widehat{MEO}=\widehat{MAO}=90^{\circ}\) ( do \( MA \) là tiếp tuyến )

\(\Rightarrow EO\) vuông góc với dây cung \( PQ \)

\(\Rightarrow E\) là trung điểm \( PQ \)

Cách chứng minh trung điểm dựa vào tính chất đối xứng

Đối xứng trục

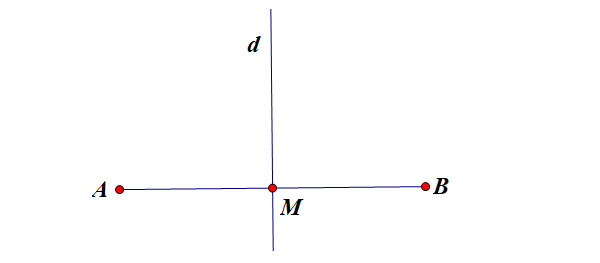
Hai điểm \( A,B \) đối xứng với nhau qua đường thẳng \( d \) nếu \( d \) là đường trung trực của \( AB \) . Khi đó \(AB \bot d\) và \( d \) đi qua trung điểm của \( AB \)

Đối xứng tâm

Hai điểm \( A,B \) đối xứng với nhau qua điểm \( O \) nếu như \( O \) là trung điểm của \( AB \)

Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp lý thuyết về chuyên đề CM trung điểm cũng như cách chứng minh trung điểm phù hợp với từng đối tượng. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chủ đề chứng minh trung điểm. Chúc bạn luôn học tốt!

Xem thêm >>> Chuyên đề phương trình chứa ẩn ở mẫu: Lý thuyết và Cách giải

Xem thêm >>> Cách xác định tâm đường tròn ngoại tiếp tam giác – Toán học lớp 9