Các dạng bài tập về cách viết phương trình tiếp tuyến
- Viết phương trình tiếp tuyến tại tiếp điểm M.
- Viết phương trình tiếp tuyến đi qua điểm A cho trước.
- Viết phương trình tiếp tuyến biết hệ số góc k.
Phương trình tiếp tuyến tại tiếp điểm \(M(x_{0},y_{0})\) có dạng:
\(y=f^{‘}(x_{0})(x-x_{0})+y_{0}\) (1)
Trong đó \(f^{‘}(x_{0})\) là đạo hàm của hàm số tại điểm \(x_{0}\).
\(x_{0}; y_{0}\) là hoành độ, tung độ của tiếp điểm M.
Như vậy với bài tập yêu cầu viết phương trình tiếp tuyến thì ta phải tìm 3 đại lượng, là: \(f'(x_{0}); x_{0} và y_{0}\)
Cách viết phương trình tiếp tuyến tại tiếp điểm
Để viết phương trình tiếp tuyến tại tiếp điểm cho trước \(M(x_{0},y_{0})\)
Cách làm: Bài toán yêu cầu viết phương trình tiếp tuyến tại tiếp điểm \(M(x_{0},y_{0})\) thì công việc cần làm là tìm \(f'(x_{0}); x_{0} và y_{0}\), trong đó \(x_{0}; y_{0}\) chính là tọa độ của điểm M, vì vậy chỉ cần tính \(f'(x_{0})\), rồi thay vào phương trình (1) là xong.
Cách viết phương trình tiếp tuyến đi qua một điểm
Cho đồ thị hàm số y=f(x), viết phương trình tiếp tuyến \(\Delta\) của đồ thị hàm số biết tiếp tuyến đi qua A(a,b)
Phương pháp:
Gọi phương trình tiếp tuyến của \(\Delta\) có dạng: \(y = f’x_{0}(x – x_{0}) + y_{0}\) (2)
Và có tiếp điểm \(M_{0}(x_{0},y_{0})\)
Vì A(a,b) thuộc tiếp tuyến nên thay tọa độ A vào phương trình ta có:
\(b = f’_{x_{0}} (a – x_{0}) + f_{x_{0}}\)
Phương trình này chỉ chứa ẩn \(x_{0}\), do đó chỉ cần giải phương trình trên để tìm \(x_{0}\)
Sau đó sẽ tìm được \(f'(x_{0}); x_{0} và y_{0}\)
Tới đây phương trình tiếp tuyến của chúng ta đã tìm được.
Cách viết phương trình tiếp tuyến có hệ số góc k
Để viết phương trình tiếp tuyến \(\Delta\) của đồ thị (C) y = f(x) khi hệ số góc k ta làm theo các bước sau:
- Bước 1: Tính đạo hàm f’(x)
- Bước 2: Giải phương trình f’(x) = k để tìm hoành độ \(x_{0}\)của tiếp điểm. Từ đây suy ra tọa độ điểm \(M_{0}(x_{0}; y_{0})\) với \(y_{0} = f(x_{0})\)
- Bước 3: Viết phương trình tiếp tuyến \(\Delta\) tại tiếp điểm \(M_{0}(x_{0}; y_{0})\)
\(y = f'(x_{0})(x – x_{0}) + y_{0}\)
***Chú ý: Tính chất của hệ số góc k của tiếp tuyến
- Tiếp tuyến song song với đường thẳng y = ax + b thì k = a
- Tiếp tuyến vuông góc với đường thẳng y = ax + b thì \(k=-\frac{1}{a}\)
Phương trình tiếp tuyến song song với đường thẳng
Vì tiếp tuyến song song với đường thẳng y=ax+b nên tiếp tuyến có hệ số góc k=a. Phương trình tiếp tuyến của (C) đi qua tiếp điểm \(M(x_{_{0}}, y_{0})\) là \(y=a(x-x_{0})+y_{0}\)
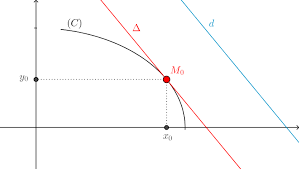
Phương trình tiếp tuyến vuông góc với đường thẳng
Vì tiếp tuyến vuông góc với đường thẳng có phương trình y=ax+b nên tiếp tuyến có hệ số góc \(k=-\frac{1}{a}\)
Phương trình tiếp tuyến của (C) đi qua tiếp điểm \(M(x_{_{0}}, y_{0})\) là \(-\frac{1}{a}(x-x_{0})+y_{0}\)