Định nghĩa nguyên hàm là gì?
Nguyên hàm là gì?
Cho hàm số \(f \) xác định trên \(K\). Hàm số \(F\) được gọi là nguyên hàm của \(f \) nếu \(F′(x)=f(x)\) với mọi x thuộc \(K\)
Chú ý : Giả sử hàm số \(F\) là một nguyên hàm của hàm số \(f \) trên \(K\) thì khi đó hàm số \(y=F(x)+C\) cũng là một nguyên hàm của \(f \) trên \(K\) với mọi hằng số \(C\)
Một số công thức nguyên hàm cơ bản
Dưới đây là một số công thức tính nguyên hàm cơ bản thường được sử dụng:
- \(\int 0dx = C\)
- \(\int dx =x+ C\)
- \(\int x^{k}dx = \frac{x^{k+1}}{k+1} +C\) với \(k \neq 1\)
- \(\int \frac{1}{x} dx =\ln |x| +C\)
- \(\int a^{x} dx = \frac{a^{x}}{\ln a} +C\) với \(0<a \neq 1\)
- Với \(k\) là hằng số khác \(0\):
\(\int \sin kx \hspace{2mm} dx = \frac{-\cos kx}{k} +C\)
\(\int \cos kx \hspace{2mm} dx = \frac{\sin kx}{k} +C\)
\(\int e^{kx} dx = \frac{e^{kx}}{k} +C\)
- \(\int \frac{1}{\cos^{2}x}dx =\tan x +C\)
- \(\int \frac{1}{\sin^{2}x}dx =-\cot x +C\)
Định nghĩa tích phân là gì?
Tích phân là gì?
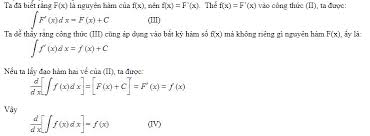
Một số quy tắc tích phân căn bản
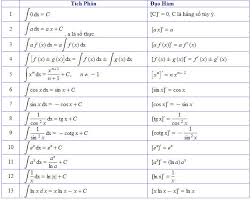
Phương pháp tính tích phân
Về lý thuyết có 3 cách tính tích phân cơ bản như sau:
- Tính tích phân bằng phương pháp phân tích.
- Tính tích phân bằng phương pháp đổi biến.
- Tính tích phân bằng phương pháp từng phần.
Bảng tích phân của một số hàm số sơ cấp dựa vào đạo hàm

Phương pháp đổi biến số trong nguyên hàm
Dạng bài thông dụng chính là tìm nguyên hàm bằng phương pháp đổi biến số. Cơ sở của phương pháp này trong nguyên hàm là ta sử dụng định lý:
Cho hàm số \(u=u(x)\) có đạo hàm liên tục trên \(K\) và hàm số \(y=f(u)\) liên tục thỏa mãn \(f[u(x)]\) xác định trên \(K\). Khi đó nếu \(F\) là một nguyên hàm của hàm số \(f\) thì :\(\int f[u(x)]u'(x)dx= F[u(x)]+C\)
Phương pháp đổi biến số dạng 1
Để tính nguyên hàm hàm số \(f(x)\) ta thực hiện các bước sau:
- Bước 1: Đặt ẩn \(t=u(x)\) trong đó \(u(x)\) là một hàm số thích hợp. Khi đó \(dt = u’(x)dx\)
- Bước 2: Biến đổi \(\int f(x)dx = \int g[u(x)].u'(x)dx =\int g(t)dt =G(t) +C\)
- Bước 3: Thay \(t=u(x)\) , ta được kết quả
Ví dụ:
Tìm \(\int \frac{x^3}{\sqrt[3]{2x^4+3}}dx\)
Cách giải:
Ta có:
\(\frac{x^3}{\sqrt[3]{2x^4+3}}dx = \frac{1}{8}.\frac{8x^3}{\sqrt[3]{2x^4+3}}dx=\frac{1}{8}.\frac{(2x^4+3)’}{\sqrt[3]{2x^4+3}}dx =\frac{1}{8}.\frac{d(2x^4+3)}{\sqrt[3]{2x^4+3}}\)
Đặt \(t=2x^4+3\) vào ta được :
\(\int \frac{x^3}{\sqrt[3]{2x^4+3}}dx = \frac{3\sqrt[3]{(2x^4+3)^2}}{16} +C\)
Phương pháp đổi biến số dạng 2
Để tính nguyên hàm hàm số \(f(x)\) ta thực hiện các bước sau:
- Bước 1: Đặt \(x=u(t)\) trong đó \(u(t)\) là một hàm số thích hợp. Khi đó \(dx=u’(t)dt\)
- Bước 2: Biến đổi \(\int f(x)dx = \int f[u(t)]u'(t)dt=\int g(t)dt=G(t)+C\)
- Bước 3: Biến đổi \(G(t)\) theo \(x\), ta được kết quả
Ví dụ:
Tìm \(\int \frac{dx}{\sqrt{(1+x^2)^3}}\)
Cách giải:
Đặt \(x=\tan t\) với \(t \in [-\frac{\pi}{2};\frac{\pi}{2}]\)
Khi đó : \(dx = (\tan t)’dt=\frac{dt}{\cos^2t}\)
Vậy ta có :
\(\int \frac{dx}{\sqrt{(1+x^2)^3}} = \int \frac{dt}{\sqrt{(1+\tan^2t)^3}.\cos^2t} =\int \cos t \hspace{2mm} dt= \sin t +C\)
Vì \(x=\tan t\) nên:
\(x^2= \frac{\sin^2 t}{\cos^2 t} = \frac{\sin^2 t}{1- \sin^2 t}\)
\(\Rightarrow x^2(1- \sin^2 t) = \sin ^2 t \Rightarrow \sin^2 t(1+x^2)= x^2\)
\(\Rightarrow \sin t = \frac{x}{\sqrt{1+x^2}}\)
Thay vào ta được : \(\int \frac{dx}{\sqrt{(1+x^2)^3}} =\frac{x}{\sqrt{1+x^2}} +C\)
Phương pháp đổi biến số trong tích phân
Phương pháp đổi biến số quy về tìm nguyên hàm
Ta áp dụng các cách đổi biến số trong nguyên hàm để tìm nguyên hàm của hàm số. Sau đó tính tính phân theo yêu cầu của đề bài
Ví dụ:
Tìm \(\int_{0}^{1} \sqrt{1-x^2} \hspace{2mm} dx\)
Cách giải:
Đặt \(x=\sin t\) với \(t \in [-\frac{\pi}{2};\frac{\pi}{2}]\)
Khi đó \(dx = (\sin t)’dt= \cos t \hspace{2mm} dt\)
Đổi cận: Với \(x=0 \Rightarrow t=0\) và \(x=1 \Rightarrow t=\frac{\pi}{2}\)
Vậy
\(\int \sqrt{1-x^2} \hspace{2mm} dx = \int \sqrt{1-\sin^2t}.\cos t \hspace{2mm} dt=\int \cos^2 t \hspace{2mm} dt\)
\(=\int \frac{\cos 2t +1}{2}dt =\frac{\sin 2t}{4} +\frac{t}{2}\)
Do đó:
\(\int_{0}^{1} \sqrt{1-x^2} \hspace{2mm} dx =\frac{\sin 2t}{4} +\frac{t}{2} \bigg|_{0}^{\frac{\pi}{2}}=\frac{\pi}{4}\)
Phương pháp đổi biến số đặc biệt
Trong một số bài toán tính tích phân \(I=\int_{a}^{b}f(x)dx\) , ta có thể đặt ẩn phụ: \(t=(a+b)-x\) sau đó lợi dụng tính chẵn lẻ của hàm số \(f(x)\) để tính toán dễ dàng hơn
Ví dụ:
Tính tích phân \(I=\int_{-1}^{1}x^{2018}\sin x \hspace{2mm} dx\)
Cách giải:
Ta có:
\(I=\int_{-1}^{1}x^{2018}\sin x \hspace{2mm} dx =\int_{-1}^{0}x^{2018}\sin x \hspace{2mm} dx + \int_{0}^{1}x^{2018}\sin x \hspace{2mm} dx \hspace{2mm} (*)\)
Đặt \(J=\int_{-1}^{0}x^{2018}\sin x \hspace{2mm} dx\)
Đặt \(t=-x \Rightarrow dx=-dt\)
Đổi cận \(x=0 \Rightarrow t=0\) và \(x=-1 \Rightarrow t=1\)
Vậy ta có :
\(J=\int_{-1}^{0}x^{2018}\sin x \hspace{2mm} dx = -\int_{0}^{1}(-t)^{2018}.\sin (-t).(-dt)= -\int_{0}^{1}t^{2018}.\sin t \hspace{2mm} dt\)
Thay vảo (\(∗\)) ta được:\( I=0\)
Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp lý thuyết về nguyên hàm, tích phân cũng như phương pháp đổi biến số trong nguyên hàm và tích phân. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho các bạn trong quá trình học tập và nghiên cứu về phương pháp đổi biến số. Chúc bạn luôn học tốt!