Ba đường thẳng đồng quy là gì?
Định nghĩa ba đường thẳng đồng quy: Cho ba đường thẳng \(a,b,c\) không trùng nhau. Khi đó ta nói ba đường thẳng \(a,b,c\) đồng quy khi ba đường thẳng đó cùng đi qua một điểm \(O\) nào đó.
Ba đường thẳng đồng quy trong mặt phẳng
Ba đường thẳng đồng quy đồ thị hàm số
Đây là dạng bài toán hàm số. để chứng minh ba đường thẳng bất kì đồng quy tại 1 điểm thì ta tìm giao điểm của hai trong số ba đường thẳng đó. Sau đó ta chứng minh đường thẳng còn lại cũng đi qua giao điểm nói trên
Ví dụ:
Trong mặt phẳng \(Oxy\) cho phương trình ba đường thẳng :
\(\left\{\begin{matrix} a: x-y+6=0\\b: 3x-y+7=0 \\ c: (m-2)x+y-1=0 \end{matrix}\right.\)
Tìm m để 3 đường thẳng đồng quy?
Cách giải:
Đầu tiên ta tìm giao điểm \(O\) của \(a\) và \(b\)
Vì \(O=a∩b⇒ \)tọa độ của \(O\) là nghiệm của hệ phương trình :
\(\left\{\begin{matrix} x-y+6=0\\ 3x-y+7=0 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x=-\frac{1}{2}\\ y=\frac{11}{2} \end{matrix}\right.\)
\(\Rightarrow O(-\frac{1}{2};\frac{11}{2})\)
Để ba đường thẳng \(a,b,c \) đồng quy thì \(O(-\frac{1}{2};\frac{11}{2}) \in c\)
\(\Rightarrow (2-m).\frac{1}{2}+\frac{11}{2}-1=0\)
\(\Leftrightarrow m=11\)
Cách chứng minh 3 đường thẳng đồng quy lớp 9
Trong các bài toán hình học phẳng THCS, để chứng minh 3 đường thẳng đồng quy thì chúng ta có thể sử dụng các phương pháp sau đây :
- Tìm giao của hai đường thẳng, sau đó chứng minh đường thẳng thứ ba đi qua giao điểm đó.
- Sử dụng tính chất đồng quy trong tam giác:
- Ba đường trung tuyến của tam giác đồng quy tại trọng tâm tam giác.
- Ba đường phân giác.đồng quy tại tâm đường tròn nội tiếp tam giác.
- Ba đường trung trực đồng quy tại tâm đường tròn ngoại tiếp tam giác.
- Ba đường cao đồng quy tại trực tâm tam giác.
- Đặc biệt ba điểm trọng tâm, trực tâm và tâm đường tròn ngoại tiếp thẳng hàng nhau. Đường thẳng đi qua ba điểm đó được gọi là đường thẳng Euler của tam giác
- Sử dụng định lý Ceva: Cho tam giác \(ABC\) và ba điểm bất kì \(M,N,P\) nằm trên ba cạnh \(BC,CA,AB\). Khi đó ba đường thẳng \(AM,BN,CP\) đồng quy khi và chỉ khi : \(\frac{MB}{MC}.\frac{NC}{NA}.\frac{PA}{PB}=1\)
.png)
- Sử dụng chứng minh phản chứng: Giả sử ba đường thẳng đã cho không đồng quy. Từ đó dẫn dắt để dẫn đến một điều vô lý
Ví dụ 1:
Cho tam giác \(ABC\). Qua mỗi đỉnh \(A,B,C\) kẻ các đường thẳng song song với cạnh đối diện, chúng lần lượt cắt nhau tại \(F,D,E\). Chứng minh rằng ba đường thẳng \(AD,BE,CF\) đồng quy.
Cách giải:
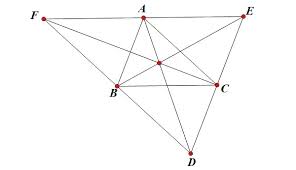
Ta có:
\(\left\{\begin{matrix} AE || BC\\AB ||CE \end{matrix}\right. \Rightarrow ABCE\) là hình bình hành
\(\Rightarrow AE=BC\)
Chứng minh tương tự ta cũng có \(ACBF\) là hình bình hành
\(\Rightarrow AF=BC\)
\(\Rightarrow AE=AF \Rightarrow\)\(A\) là trung điểm \(EF\)
Tương tự ta cũng có :\( B\) là trung điểm \(DF\)
\(C\) là trung điểm \(DE\)
Như vậy, \(A,B,C\) là trung điểm của ba cạnh tam giác \(DEF\)
Do đó\( ⇒AD,BE,CF\) đồng quy tại trọng tâm tam giác \(DEF\)
Ví dụ 2:
Cho tam giác \(ABC\) có đường cao \(AH\). Lấy \(D,E\) nằm trên\( AB,AC\) sao cho \(AH\) là phân giác của góc \(\widehat{DHE}\). Chứng minh ba đường thẳng \(AH,BE,CD\) đồng quy.
Cách giải:
.png)
Qua \(A\) kẻ đường thẳng song song với \(BC\) cắt \(HD,HE\) lần lượt tại \(M,N\)
Vì \(\left\{\begin{matrix} MN || BC \\ AH \bot BC \end{matrix}\right. \Rightarrow AH \bot MN\)
Mặt khác \(AH\) lại là phân giác góc \(\widehat{MHN}\)
\(⇒AH\) vừa là đường cao, vừa là phân giác của tam giác \(MHN\)
\(⇒ΔMHN\) cân tại \(H\) và \(AH\) cũng là đường trung tuyến của \(MN\)
\(⇒AM=AN\)(1)
Do \(MN||BC\) nên ta có :
\(\Delta DMA \sim \Delta DHB \Rightarrow \frac{AD}{BD}=\frac{MA}{HB} \;\;\;\;(2)\)
Tương tự ta cũng có:
\(\Delta ENA\sim \Delta EHC\Rightarrow \frac{AE}{CE}=\frac{NA}{HC} \;\;\;\;(3)\)
Từ \((1)(2)(3)\) ta có :
\(\frac{DA}{DB}.\frac{HB}{HC}.\frac{EC}{EA}=\frac{MA}{HB}.\frac{HB}{HC}.\frac{HC}{NA}=\frac{AM}{AN}=1\)
Vậy áp dụng định lý Ceva cho \(ΔABC⇒\) ba đường thẳng \(AH,BE,CD\) thẳng hàng.
Ba đường thẳng đồng quy trong không gian
Trong không gian cho ba đường thẳng \(a,b,c\). Để chứng minh ba đường thẳng này cắt nhau ta có thể sử dụng hai cách sau đây :
- Cách 1:
Tìm \(I=a∩b\)
Tìm hai mặt phẳng \((P),(Q)\) chứa \(I \) thỏa mãn \(c=(P)∩(Q)\). Khi đó hiển nhiên \(I∈c\)
- Cách 2:
Ta áp dụng định lý : Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến thì 3 giao tuyến đó song song hoặc đồng quy
Áp dụng vào bài toán, ta chỉ cần chứng minh ba đường thẳng \(a,b,c\) không đồng phẳng và cắt nhau đôi một
Ví dụ 1:
Cho hai hình bình hành \(ABCD,ABEF\) thuộc hai mặt phẳng khác nhau. Trên các đoạn thẳng \(EC,DF\) lần lượt lấy hai điểm \(M,N\) sao cho \(AM,BN\) cắt nhau. Gọi \(I,K\) lần lượt là giao điểm các đường chéo của hai hình bình hành. Chứng minh rằng ba đường thẳng \(IK,AM,BN\) đồng quy.
Cách giải:
Gọi \(O=AM∩BN\)
Xét hai mặt phẳng \((ACE),(BDF) \)ta có :
\(\left\{\begin{matrix} AC\cap BD =I\\ AE \cap BF =K \end{matrix}\right. \Rightarrow IK =(AEC)\cap (BDF) \;\;\;\; (1)\)
Mặt khác ta lại có :
\(\left\{\begin{matrix} O=AM\cap BN \\ AM \in (AEC)\\ BN \in (BDF) \end{matrix}\right. \Rightarrow O\) nằm trên cả hai mặt phẳng \((ACE),(BDF)\) (2)
Từ (\(1)(2)⇒O∈KI\)
Vậy \(AM,BN,KI\) đồng quy tại \(O\)
Ví dụ 2: Tìm m để 3 đường thẳng đồng quy.
Tìm m để \((d1): y = 2x + 1\); \((d2): y= -x-2\) ; \((d3): y=(m-1)x – 4\)
Hãy tìm m để 3 đường thẳng đồng quy và vẽ hình để minh họa.
Cách giải:
Xét phương trình hoành độ giao điểm của \((d1)\) và \((d2)\)
\(y = 2x + 1 = -x-2\)
\(⇔ 3x = -3 ⇔ x = -1\)
Suy ra ta có \(y = 2(-1) + 1 = -1\)
Như vậy giao điểm của (d1) và (d2) là\( I(-1;-1)\)
Để ba đường thẳng trên đồng quy (cùng giao nhau tại một điểm) thì điểm \( I\) phải thuộc đường thẳng (d3)
\(=> -1 = (m – 1)(-1) – 4\)
\(⇔ m = -2\)
Khi đó thì phương trình đường thẳng \((d3): y = -3x – 4\)
Bài tập ba đường thẳng đồng quy
Sau đây là một số bài tập về 3 đường thẳng đồng quy để bạn đọc có thể tự rèn luyện :
Tìm m để 3 đường thẳng đồng quy toán 9
Trong mặt phẳng Oxy cho ba đường thẳng :
\(\left\{\begin{matrix} d_1: y=2x+1\\ d_2: y=-x-2 \\ d_3: (m-1)x-4 \end{matrix}\right.\)
Tìm giá trị của m để ba đường thẳng trên đồng quy.
Chứng minh ba đường thẳng cùng đồng quy
Cho tứ giác lồi \(ABCD\) và tam giác \(ABM\) nằm trong hai mặt phẳng khác nhau. Trên các cạnh \(MA,MB\) của tam giác \(MAB\) ta lấy các điểm tương ứng \(A′,B′\) sao cho các đường thẳng \(CA′,DB′\) cắt nhau. Gọi \(H\) là giao điểm hai đường chéo của tứ giác \(ABCD\) .Chứng minh rằng các đường thẳng \(MH,CA′,DB′\) đồng quy.
Ba đường thẳng cùng đồng quy tại một điểm
Qua các điểm \(A,D\) nằm trên đường tròn kẻ các đường tiếp tuyến, chúng cắt nhau taị điểm \(S\). Trên cung \(AD\) lấy các điểm \(A,B\). Các đường thẳng \(AC,BD\) cắt nhau taị điểm \(P\) . Chứng minh rằng ba đường thẳng \(AB,CD,SP \)đồng quy
Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp lý thuyết cũng như phương pháp chứng minh 3 đường thẳng đồng quy. Hy vọng kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chủ đề ba đường thẳng đồng quy. Chúc bạn luôn học tốt!
