Các dạng phương trình lượng giác
Phương trình sinx = m
Nếu |m|>1: Phương trình vô nghiệm
Nếu |m| ≤ 1 thì chọn 1 góc α sao cho sinα=m.
Khi đó nghiệm của phương trình là \(\left\{\begin{matrix} x = \alpha + k2\pi & \\ x = \pi – \alpha +k2\pi & \end{matrix}\right.\) với \(k \epsilon \mathbb{Z}\)
Phương trình cosx = m
Nếu |m|>1: Phương trình vô nghiệm
Nếu |m| ≤ 1 thì chọn 1 góc α sao cho cosα=m .
Khi đó nghiệm của phương trình là \(\left\{\begin{matrix} x = \alpha + k2\pi & \\ x = – \alpha + k2\pi & \end{matrix}\right.\)với \(k \epsilon \mathbb{Z}\)
Phương trình tanx = m
Chọn góc α sao cho tanα=m.
Khi đó phương trình luôn có nghiệm với mọi m.
\(\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi (k \epsilon \mathbb{Z})\)
Hoặc \(\tan x = m \Leftrightarrow m – \arctan m + k\pi\) (m bất kỳ)
Chú ý: \(\tan x = 0 \Leftrightarrow x = k\pi\) không xác định khi \(x = \frac{\pi }{2} + k\pi\)
Phương trình cot(x) = m
Chọn góc \(α\) sao cho \(cosα=m\).
Khi đó phương trình luôn có nghiệm với mọi m.
\(\cos x = \cos \alpha \Leftrightarrow x = \alpha + k\pi (k\epsilon \mathbb{Z})\) hoặc \(\cot x = m \Leftrightarrow m = \textrm{arccsc}m + k\pi\) (m bất kỳ)
Chú ý: \(\csc x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi\)
\(cscx\) không xác định khi \(x=kπ\)
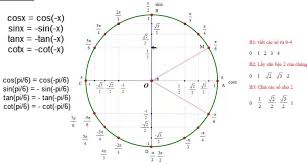
Vòng tròn lượng giác cho các bạn tham khảo:
Phương trình lượng giác chứa tham số
Phương trình lượng giác chứa tham số dạng \(a\sin x + b \cos x = c\) có nghiệm khi và chỉ khi \(a^{2} + b^{2} \geq c^{2}\)
Để giải phương trình lượng giác chứa tham số có hai cách làm phổ biến là:
- Thứ nhất đưa về PT lượng giác cơ bản
- Thứ hai sử dụng phương pháp khảo sát hàm
Phương pháp 1: Đưa về dạng phương trình lượng giác cơ bản
- Điều kiện có nghiệm của phương trình lượng giác
- Kết hợp những kiến thức đã học đưa ra các điều kiện làm cho phương trình dạng cơ bản có nghiệm thỏa điều kiện cho trước
Ví dụ: Xác định m để phương trình \((m^{2} – 3m + 2)\cos ^{2}x = m(m-1)\) (1) có nghiệm.
Cách giải
\((1)\Leftrightarrow (m-1)(m-2)\cos ^{2}x = m (m-1)\) (1’)
Khi m = 1: (1) luôn đúng với mọi \(x\epsilon \mathbb{R}\)
Khi m = 2: (1) vô nghiệm
Khi \(m\neq 1; m\neq 2\) thì:
(1’) \(\Leftrightarrow (m-2)\cos ^{2}x = m \Leftrightarrow \cos ^{2}x = \frac{m}{m-2}\) (2)
Khi đó (2) có nghiệm \(\Leftrightarrow 0\leq \frac{m}{m-2}\leq 1\Leftrightarrow m\leq 0\)
Vậy (1) có nghiệm khi và chỉ khi m = 1, \(m\leq 0\)
Phương pháp 2: Sử dụng phương pháp khảo sát
Giả sử phương trình lượng giác chứa tham số m có dạng: g(x,m) = 0 (1). Xác định m để phương trình (1) có nghiệm \(xϵD\)
Phương pháp:
- Đặt ẩn phụ t = h(x) trong đó h(x) là 1 biểu thức thích hợp trong phương trình (1)
- Tìm miền giá trị (điều kiện) của t trên tập xác định D. Gọi miền giá trị của t là D1
- Đưa phương trình (1) về phương trình f(m,t) = 0
- Tính f’(m, t) và lập bảng biến thiên trên miền D1
- Căn cứ vào bảng biến thiên và kết quả của bước 4 mà các định giá trị của m.
Trên đây là bài tổng hợp kiến thức về phương trình lượng giác của DINHNGHIA.VN. Nếu có góp ý hay băn khoăn thắc mắc gì các bạn bình luận bên dưới nha.Cảm ơn các bạn! Nếu thấy hay thì chia sẻ nhé ^^